(FUVEST)
Um sistema industrial é constituído por
um tanque cilíndrico, com 600 litros de água e área de fundo S1 = 0,6 m2, e por um balde, com área do
fundo S2 = 0,2 m2. O balde está vazio e é mantido
suspenso, logo acima do nível da água do tanque, com auxílio de um fino fio de
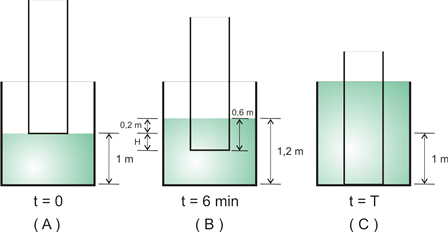
aço e de um contrapeso C, como indicado na figura. Então, em t = 0 s, o balde passa a receber água de
uma torneira, à razão de 20 litros por minuto, e vai descendo, com velocidade
constante, até que encoste no fundo do tanque e a torneira seja
fechada.
Para o instante t = 6 minutos,
com a torneira aberta, na situação em que o balde ainda não atingiu o fundo,
determine:
a) A tensão adicional ΔF, em N,
que passa agir no fio que sustenta o balde, em relação à situação inicial,
indicada na figura.
b) A
altura da água H6, em
m, dentro do tanque.
c)
Considerando todo o tempo em que a torneira fica aberta, determine o intervalo
de tempo T, em minutos, que o balde leva para encostar no fundo do
tanque.
Note e
adote:
O contrapeso equilibra o peso do balde,
quando vazio.
O volume das paredes do balde é
desprezível.
Resolução:
a) Se o balde desce com
velocidade constante, concluímos que o contrapeso sobe com velocidade constante.
Nestas condições, a intensidade da força de tração no fio é sempre igual ao peso
do contrapeso. Deste modo, a intensidade da força de tração no fio não varia e
portanto: ΔF = 0.
b) Para
que a intensidade da força de tração no fio não varie, devemos concluir que, em
cada instante, o peso da água colocada no balde é igual à intensidade do empuxo,
isto é o peso da água colocada no baldo é igual ao peso da água deslocada. Por
isso, o nível da água no balde é o mesmo nível da água no tanque. No instante 6
min o balde recebeu o seguinte volume de água:
20 (litros/minuto) x 6 minutos
= 120 litros
O volume total de água no tanque é de: 600 litros + 120 litros =
720 litros
A altura H6
de água no tanque será:
Vtotal
= S1.H6 =>
720.10-3 =
0,6.H6
=> H6 =
1,2 m
c) altura da água no tanque, no instante t = 0 (figura
A):
V1 =
S1.H1
=> 600.10-3 =
0,6.h1
=> h1
= 1 m
Altura da água no balde no instante t = 6 min (figura B)
V2 =
S2.H2
=> 120.10-3
= 0,2.h2
=> h2
= 0,6 m
Observando as posições da base do tanque entre os instantes t = 0 e t
= 6 min, concluímos que o tanque desce a distância H = 0,4 m. Logo a velocidade
de descida do tanque é:
V = 0,4 m/6 min
Entre os instantes t = 0 e t = T
(figura C), a base do tanque desce 1 m. Logo:
V = 0,4 m/6 min = 1 m/T => T
= 15 min
Respostas:
a) nula; b) 1,2 m; c) 15 min


Nenhum comentário:
Postar um comentário