Resumo:
Quando um corpo descreve um movimento circular uniforme sua aceleração é centrípeta (acp), com intensidade dada por acp = v2/R , onde v é a velocidade escalar e R o raio da trajetória.
Pela segunda lei de Newton a resultante das forças que agem no corpo, chamada resultante centrípeta (Fcp = m.acp), é responsável pela trajetória circular que o corpo descreve. Fcp e acp têm direção perpendicular à velocidade vetorial do corpo, em cada instante e sentido para o centro da trajetória.
Exemplos:
1) Um pequeno bloco preso a um fio descreve em uma mesa, perfeitamente lisa, um movimento circular uniforme. As forças que agem no bloco são: o peso P, a força normal FN e a força de tração T. O peso e a força normal se equilibram. A resultante é a força de tração. Ela é a resultante centrípeta.
2) Num pêndulo cônico uma pequena esfera, presa a um fio, descreve uma trajetória circular num plano horizontal. As forças que agem na esfera são: o peso P e a força de tração T. A resultante P + T é a resultante centrípeta.
Se o movimento curvilíneo for variado a força resultante apresenta duas componentes, uma centrípeta (responsável pela variação da direção da velocidade) e outra tangencial (responsável pela variação do módulo da velocidade). Veja o exemplo: uma pequena esfera presa a um fio oscila num plano vertical (pêndulo simples). Observe a esfera ao passar pela posição C. As forças que nela agem são o peso P e a força de tração T. Vamos decompor o peso nas componentes Pt e Pn.
O módulo da resultante centrípeta é T - Pn e o módulo da resultante tangencial é Pt.
Animações:
Clique aqui e aqui
Exercícios básicos
Exercício 1:
Um motociclista com sua moto descreve uma trajetória circular de raio R, num plano vertical, no interior de um globo da morte. O motociclista realiza a volta completa, sem descolar do piso. Prove que, nestas condições, a velocidade mínima do motociclista no ponto mais alto da trajetória é dada por
onde g é a aceleração local da gravidade.
Resolução:
m.g + FN = m.v2/R
vmin => FN = 0
m.g = m.(vmin)2/R
Exercício 2:
Um carro de massa m entra numa curva de raio R de uma estrada horizontal. O coeficiente de atrito estático entre a pista e os pneus é igual a μ. Prove que a máxima velocidade com que o carro pode fazer a curva, sem o perigo de derrapar, é dada por
onde g é a aceleração local da gravidade.
Resolução:
Fat = m.v2/R ≤ μ.FN m.v2/R ≤ μ.m.gv2 ≤ μ.R.g
Exercício 3:
Um automóvel percorre uma pista curva sobrelevada, isto é, a curva apresenta a margem externa mais elevada do que a margem interna. Seja θ o ângulo de sobrelevação, tal que tg θ = 0,15. Com que velocidade escalar o automóvel deve efetuar a curva, independentemente da força de atrito entre os pneus e a pista? É dada a aceleração da gravidade g =10 m/s2 e o raio da trajetória R = 150 m.
Clique para ampliar
Exercício 4:
Um avião realiza um movimento circular uniforme de raio R = 120 m e com velocidade escalar v = 40 m/s. F é a força de sustentação e P é o peso do avião. Determine a intensidade da força F em função da massa m do avião. Considere
Resolução:
Na figura representamos as forças que agem no carro e a força resultante FR que é centrípeta:
No triângulo sombreado temos:
tg θ = FR/P = (m.v2/R)/m.g => tg θ = v2/R.g => 0,15 = v2/1500 =>
v = 15 m/s
Resposta: 15 m/s
No triângulo sombreado temos:
tg θ = FR/P = (m.v2/R)/m.g => tg θ = v2/R.g => 0,15 = v2/1500 =>
v = 15 m/s
Resposta: 15 m/s
Exercício 4:
g = 10 m/s2.
Resolução:
Na figura representamos as forças que agem no avião e a força resultante FR que é centrípeta:
P = m.g => P = 10.m e FR = (m.v2/R) => FR = m.[(40)2/120] => FR = 40.m/3
Pelo Teorema de Pitágoras, temos:
F2 = P2 +(FR)2 => F2 = 100.m2 + 1600.m2/9 => F2 = 2500.m2/9 =>
F = 50.m/3
Resposta: 50.m/3
Exercício 5:
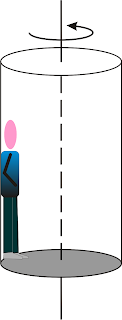
O rotor é um cilindro oco que pode girar em torno de seu eixo. Uma pessoa está encostada na parede interna do cilindro, conforme mostra a figura. O cilindro começa a girar e a pessoa gira junto como se ficasse "grudada" no cilindro. Quando atinge uma velocidade angular mínima ωmin o piso é retirado e a pessoa não cai. Seja R o raio do cilindro, g a aceleração local da gravidade e μ o coeficiente de atrito estático entre a roupa da pessoa e a parede do cilindro.
x
a) Represente as forças que agem na pessoa: o peso P e as componentes Fat (força de atrito) e FN (força normal).b) Prove que
Resolução:
Revisão/Ex 1:
(VUNESP)
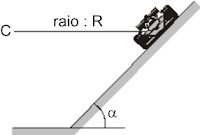
Curvas com ligeiras inclinações em circuitos automobilísticos são indicadas para aumentar a segurança do carro a altas velocidades, como, por exemplo, no Talladega Superspeedway, um circuito utilizado para corridas promovidas pela NASCAR (National Association for Stock Car Auto Racing). Considere um carro como sendo um ponto material percorrendo uma pista circular, de centro C, inclinada de um ângulo α e com raio R, constantes, como mostra a figura, que apresenta a frente do carro em um dos trechos da pista.
a) não possui aceleração vetorial.
b) possui aceleração com módulo variável, direção radial e no sentido
para o ponto C.
c) possui aceleração com módulo variável e tangente à trajetória circular.
d) possui aceleração com módulo constante, direção radial e no sentido
para o ponto C.
e) possui aceleração com módulo constante e tangente à trajetória circular.
Resolução:
O carro realiza um movimento circular e uniforme. Sua aceleração é centrípeta. Esta possui módulo constante, direção radial e sentido apontando para o centro C.
Resposta: d
Revisão/Ex 2:
(FGV)
Em um dia muito chuvoso, um automóvel, de massa m, trafega por um trecho horizontal e circular de raio R. Prevendo situações como essa, em que o atrito dos pneus com a pista praticamente desaparece, a pista é construída com uma sobre-elevação externa de um ângulo α, como mostra a figura. A aceleração da gravidade no local é g.
A máxima velocidade que o automóvel, tido como ponto material, poderá desenvolver nesse trecho, considerando ausência total de atrito, sem derrapar, é dada por
a) √(m.g.R.tg α)
b) √(m.g.R.cos α)
c) √(g.R.tg α)
d) √(g.R.cos α)
e) √(g.R.sen α)
Resolução:
tg α = FR/P = (m.v2/R)/m.g => tg α = v2/g.R => v = √(g.R.tg α)
Resposta: c
Revisão/Ex 3:
(PUC-Campinas)
Num trecho retilíneo de uma pista de automobilismo há uma lombada cujo raio de curvatura é de 50 m. Um carro passa pelo ponto mais alto da elevação com velocidade v, de forma que a interação entre o veículo e o solo (peso aparente) é m.g/5 neste ponto. Adote g = 10 m/s2.
Nestas condições, em m/s, o valor de v é
a) 10
b) 20
c) 30
d) 40
e) 50
As forças que agem no veículo são o peso de módulo P = mg e a força normal de módulo FN que é igual ao peso aparente, isto é, FN = mg/5.
Assim, temos:
Fresultante = m.acp => mg-mg/5 = m.v2/R =>
4mg/5 = m.v2/R => v2 = 4gR/5 => v2 = 4.10.50/5 => v = 20 m/s
Resposta: b


















Nenhum comentário:
Postar um comentário