Tensão superficial

Ao colocarmos uma pequena colher de aço num recipiente com água ela afunda, pois a densidade do aço é maior do que a da água. Mas por que ao colocarmos horizontalmente, com cuidado, uma agulha de aço sobre a superfície da água, ela não afunda? A resposta é que a superfície da água comporta-se como uma membrana elástica em tensão que resiste a se romper.

Este fenômeno é denominado tensão superficial e ocorre não só com a água, mas também com outros líquidos.

Como se explica a formação desta membrana? Considere uma molécula A de água no interior e outra B, na superfície. A molécula interna A está em equilíbrio sob ação das forças de coesão exercidas pelas moléculas que a rodeiam. Já a molécula B está sujeita a forças de coesão por partes das moléculas superficiais e daquelas que estão abaixo. A resultante das forças de coesão que age em B esta orientada para baixo. Assim, a camada superficial funciona como uma membrana, comprimindo as moléculas de baixo.

Devido a este fenômeno a área superficial de um líquido tende a tornar-se a menor possível. Por isso, na ausência de forças externas as gotas de um líquido tendem a assumir a forma esférica que é a de menor área para um dado volume. No interior das naves espaciais, devido a imponderabilidade, as gotas de qualquer líquido solto no ambiente, assumem a forma esférica.

Os detergentes diminuem a tensão superficial da água, permitindo que ela penetre com maior facilidade em locais de difícil acesso como cantos e orifícios pequenos, o que auxilia na limpeza de utensílios. Uma agulha colocada na superfície da água e suportada pela tensão superficial afunda quando algumas gotas de detergente são despejadas no recipiente.

O efeito Bernoulli

Uma propriedade dos fluidos em movimento, denominada Efeito Bernoulli, afirma que “onde a velocidade de um fluido é maior, a pressão é menor”. Vamos citar alguns exemplos que ilustram o efeito Bernoulli.

• Soprando uma tira de papel de seda

Ao soprar uma tira de papel de seda, conforme indica a figura, a velocidade do ar na região acima da tira é maior do que na região abaixo e consequentemente a pressão na região superior é menor. Por isso, a tira se eleva.

Clique para ampliar

• Caminhão transportando carga

É muito comum observarmos um caminhão utilizar um encerado para cobrir a carga que transporta. Estando o caminhão parado, o encerado é plano. Ao se movimentar, o encerado estufa para fora. Isto ocorre pois quando caminhão está em movimento a velocidade do ar acima do encerado é maior do que a do ar interno. Logo, a pressão do ar na região acima do encerado é menor do que a pressão interna. A diferença de pressão gera uma força para cima.

Clique para ampliar

• Destelhamento

Analogamente à situação anterior, pode haver destelhamento de uma casa durante uma ventania. Tal fato é ocasionado pela diferença de pressão do ar acima e abaixo do telhado.

• Vento rasante numa janela

Você já deve observado, durante uma ventania, que quando o ar passa rasante a uma janela, a cortina desloca-se em direção à janela.

• Animais que vivem em tocas

Eles constroem suas tocas com mais de uma abertura e em níveis diferentes. No nível mais alto a velocidade do vento é maior e a pressão é menor. A diferença de pressão entre as aberturas permite a circulação do ar.

Clique para ampliar

ACHEI INTERESSANTE!

(FUVEST)
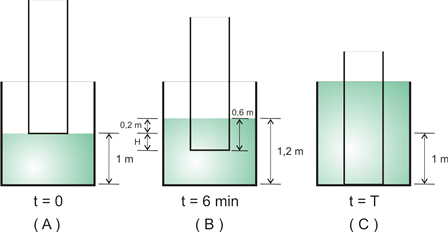
Um sistema industrial é constituído por um tanque cilíndrico, com 600 litros de água e área de fundo S₁ = 0,6 m², e por um balde, com área do fundo S₂ = 0,2 m². O balde está vazio e é mantido suspenso, logo acima do nível da água do tanque, com auxílio de um fino fio de aço e de um contrapeso C, como indicado na figura. Então, em t = 0 s, o balde passa a receber água de uma torneira, à razão de 20 litros por minuto, e vai descendo, com velocidade constante, até que encoste no fundo do tanque e a torneira seja fechada.

Para o instante t = 6 minutos, com a torneira aberta, na situação em que o balde ainda não atingiu o fundo, determine:

a) A tensão adicional ΔF, em N, que passa agir no fio que sustenta o balde, em relação à situação inicial, indicada na figura.
b) A altura da água H₆, em m, dentro do tanque.
c) Considerando todo o tempo em que a torneira fica aberta, determine o intervalo de tempo T, em minutos, que o balde leva para encostar no fundo do tanque.

Note e adote:
O contrapeso equilibra o peso do balde, quando vazio.
O volume das paredes do balde é desprezível.

Resolução:

a) Se o balde desce com velocidade constante, concluímos que o contrapeso sobe com velocidade constante. Nestas condições, a intensidade da força de tração no fio é sempre igual ao peso do contrapeso. Deste modo, a intensidade da força de tração no fio não varia e portanto: ΔF = 0.

b) Para que a intensidade da força de tração no fio não varie, devemos concluir que, em cada instante, o peso da água colocada no balde é igual à intensidade do empuxo, isto é o peso da água colocada no baldo é igual ao peso da água deslocada. Por isso, o nível da água no balde é o mesmo nível da água no tanque. No instante 6 min o balde recebeu o seguinte volume de água:
20 (litros/minuto) x 6 minutos = 120 litros
O volume total de água no tanque é de: 600 litros + 120 litros = 720 litros
A altura H₆ de água no tanque será:
V_total = S₁.H₆ => 720.10^-3 = 0,6.H₆ => H₆ = 1,2 m

c) altura da água no tanque, no instante t = 0 (figura A):
V₁ = S₁.H₁ => 600.10^-3 = 0,6.h₁ => h₁ = 1 m
Altura da água no balde no instante t = 6 min (figura B)
V₂ = S₂.H₂ => 120.10^-3 = 0,2.h₂ => h₂ = 0,6 m
Observando as posições da base do tanque entre os instantes t = 0 e t = 6 min, concluímos que o tanque desce a distância H = 0,4 m. Logo a velocidade de descida do tanque é:
V = 0,4 m/6 min
Entre os instantes t = 0 e t = T (figura C), a base do tanque desce 1 m. Logo:
V = 0,4 m/6 min = 1 m/T => T = 15 min

Respostas: a) nula; b) 1,2 m; c) 15 min